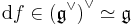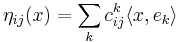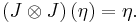Poisson manifold
In mathematics, a Poisson manifold is a differentiable manifold M such that the algebra 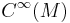 of smooth functions over M is equipped with a bilinear map called the Poisson bracket, turning it into a Poisson algebra. Since their introduction by André Lichnerowicz in 1977,[1] Poisson geometry and the cohomology of Poisson manifolds have developed into a wide field of research.
of smooth functions over M is equipped with a bilinear map called the Poisson bracket, turning it into a Poisson algebra. Since their introduction by André Lichnerowicz in 1977,[1] Poisson geometry and the cohomology of Poisson manifolds have developed into a wide field of research.
Every symplectic manifold is a Poisson manifold but not vice versa.
Contents |
Definition
A Poisson structure on M is a bilinear map
such that the bracket is skew symmetric:
obeys the Jacobi identity:
and is a derivation of C∞(M) in its first argument:
The last property allows several equivalent formulations. Fixing a smooth function g ∈ C∞(M), one has that the map f ↦ {f, g} is a derivation on C∞(M). This implies the existence of a Hamiltonian vector field Xg on M such that
for all f ∈ C∞(M). This implies that the bracket depends only on the differential of f. Thus, associated with any Poisson structure is a map from the cotangent bundle T∗M to the tangent bundle TM,
which maps df to Xf.
Poisson bivector
The map between the cotangent and tangent bundles implies the existence of a bivector field η on M, the Poisson bivector, a skew-symmetric 2-tensor 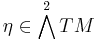 , such that
, such that
where 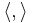 is the pairing between the tangent bundle and its dual. Conversely, given a smooth bivector field η on M, this formula can be used to define a skew-symmetric bracket which is a derivation in each argument. This bracket obeys the Jacobi identity, and hence defines a Poisson structure if and only if the Schouten–Nijenhuis bracket [η,η] is zero.
is the pairing between the tangent bundle and its dual. Conversely, given a smooth bivector field η on M, this formula can be used to define a skew-symmetric bracket which is a derivation in each argument. This bracket obeys the Jacobi identity, and hence defines a Poisson structure if and only if the Schouten–Nijenhuis bracket [η,η] is zero.
In local coordinates, the bivector at a point x = (x1, ..., xm) has the expression
so that
For a symplectic manifold, η is nothing other than the pairing between tangent and cotangent bundle induced by the symplectic form ω, which exists because it is nondegenerate. The difference between a symplectic manifold and a Poisson manifold is that the symplectic form must be nowhere singular, whereas the Poisson bivector does not need to be of full rank everywhere. When the Poisson bivector is zero everywhere, the manifold is said to possess the trivial Poisson structure.
Poisson map
A Poisson map is defined as a smooth map φ: M → N, which maps the Poisson manifold M to the Poisson manifold N, in such a way that the product structure is preserved:
where { , }M and { , }N are the Poisson brackets on M and N respectively.
Product manifold
Given two Poisson manifolds M and N, a Poisson bracket may be defined on the product manifold. Letting f1 and f2 be two smooth functions defined on the product manifold M × N, one defines the Poisson bracket { , }M×N on the product manifold in terms of the brackets { , }M and { , }N on each of the individual manifolds:
where x ∈ M and y ∈ N are held constant; that is, so that when
then
and
is implied.
Symplectic leaves
A Poisson manifold can be split into a collection of symplectic leaves. Each leaf is a submanifold of the Poisson manifold, and each leaf is a symplectic manifold itself. Two points lie in the same leaf if they are joined by a piecewise smooth curve, where each piece is the integral curve of a Hamiltonian vector field. That is, the relation "piecewise connected by integral curves of Hamiltonian fields" is an equivalence relation on the manifold. The equivalence classes of this relation are the symplectic leaves.
Example
If  is a finite-dimensional Lie algebra, and
is a finite-dimensional Lie algebra, and 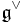 is its dual vector space, then the Lie bracket induces a Poisson structure on
is its dual vector space, then the Lie bracket induces a Poisson structure on 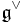 .
.
More precisely, we identify the cotangent bundle of the manifold 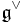 , ie the dual of
, ie the dual of 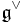 to the Lie algebra
to the Lie algebra  . Then for two functions f1 and f2 on
. Then for two functions f1 and f2 on 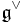 , and a point
, and a point 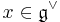 , one may define
, one may define
where the Lie bracket [ , ] is computed in  through the isomorphism:
through the isomorphism:
If ek are the local coordinates on the Lie algebra  , then the Poisson bivector is given by
, then the Poisson bivector is given by
where the 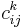 are the structure constants of the Lie algebra.
are the structure constants of the Lie algebra.
The symplectic leaves of this Poisson algebra are the coadjoint orbits of the Lie algebra used for the orbit method.
Complex structure
A complex Poisson manifold is a Poisson manifold with a complex or almost complex structure J such that the complex structure preserves the bivector:
The symplectic leaves of a complex Poisson manifold are pseudo-Kähler manifolds.
See also
Notes
- ^ Lichnerowicz, A. (1977). "Les variétés de Poisson et leurs algèbres de Lie associées". J. Diff. Geom. 12 (2): 253–300. MR0501133.
References
- Lichnerowicz, A. (1977). "Les variétés de Poisson et leurs algèbres de Lie associées". J. Diff. Geom. 12 (2): 253–300. MR0501133.
- Kirillov, A. A. (1976). "Local Lie algebras". Russ. Math. Surv. 31 (4): 55–75. doi:10.1070/RM1976v031n04ABEH001556.
- Guillemin, V.; Sternberg, S. (1984). Symplectic Techniques in Physics. New York: Cambridge Univ. Press. ISBN 0521248663.
- Libermann, P.; Marle, C.-M. (1987). Symplectic geometry and analytical mechanics. Dordrecht: Reidel. ISBN 9027724385.
- Bhaskara, K. H.; Viswanath, K. (1988). Poisson algebras and Poisson manifolds. Longman. ISBN 0-582-01989-3.
- Vaisman, I. (1994). Lectures on the Geometry of Poisson Manifolds. Birkhäuser. See also the review by Ping Xu in the Bulletin of the AMS.
- Weinstein, A. (1983). "The local structure of Poisson manifolds". J. Diff. Geom. 18 (3): 523–557. MR834280. Errata and addenda J. Diff. Geom. 22 (1985), 255.
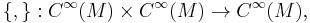
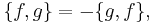
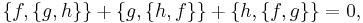
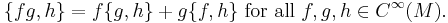
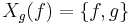
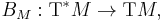
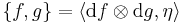
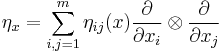
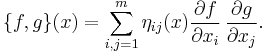
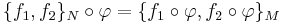
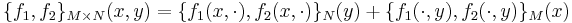
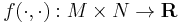
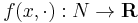
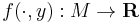
![\{f_1,f_2\}(x) = \left \langle \;\left [(\mathrm{d} f_1)_x, (\mathrm{d} f_2)_x \right ] \,, x \right \rangle](/2012-wikipedia_en_all_nopic_01_2012/I/523ce3241bd0793327ce4f46c5e92fc0.png)